Do you ever feel like O Level and IGCSE Math have you spinning in circles? Well, don't fret because this blog is here to help you regain your balance on the Mathematical tightrope. We're diving deep into the properties of circle O Level & IGCSE style. So, grab your compass, and let's navigate the circle properties rules together.
What are the Properties of a Circle?
Let's start with the basics. Here, we will explore a few, and by the end, you'll be a circle whisperer yourself.
Angles and circles, they're like cousins at a family reunion, bringing some 'degree' of fun. Now, let's dive into the angle properties of circles to uncover the world of circle properties!
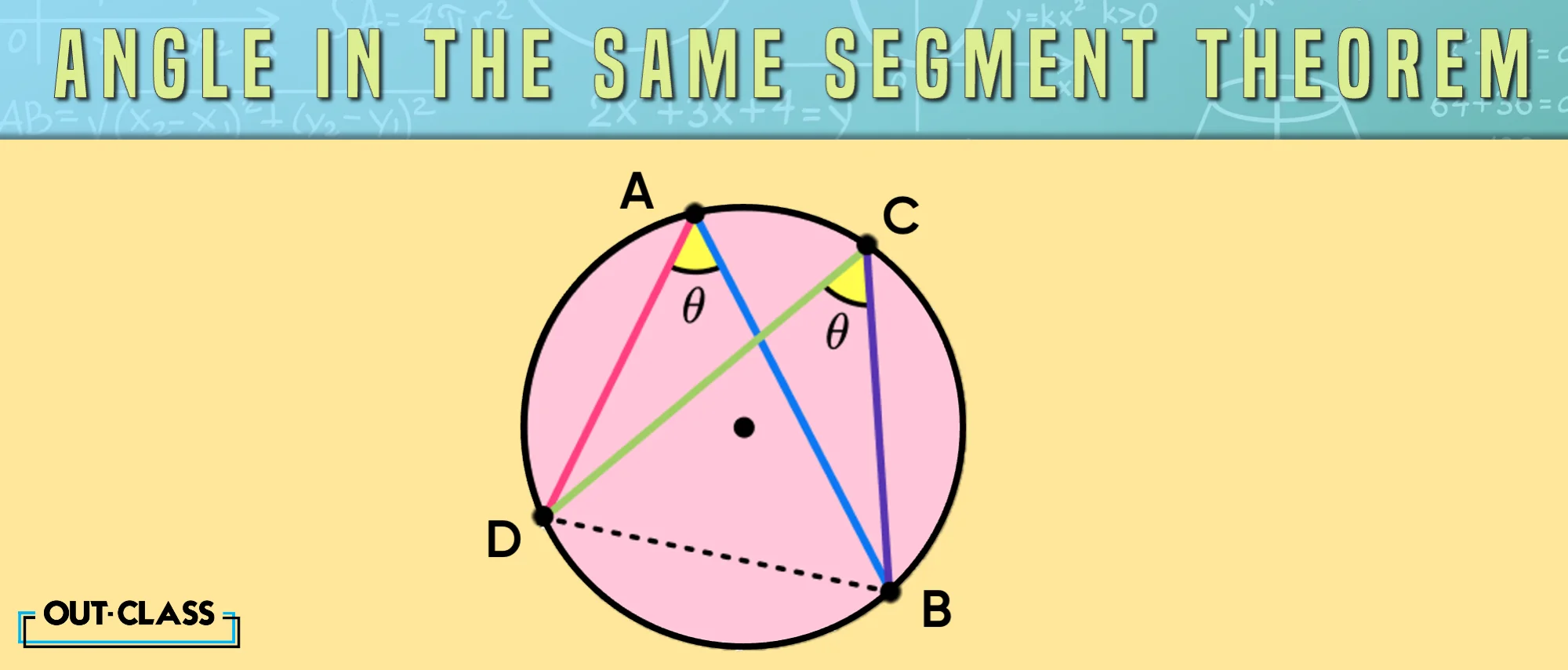
The Angle in the Same Segment Theorem:
Imagine this theorem as a circle saying, "What happens in the same segment stays in the same segment!" It means that they are equal if two angles subtend the same arc in a circle.
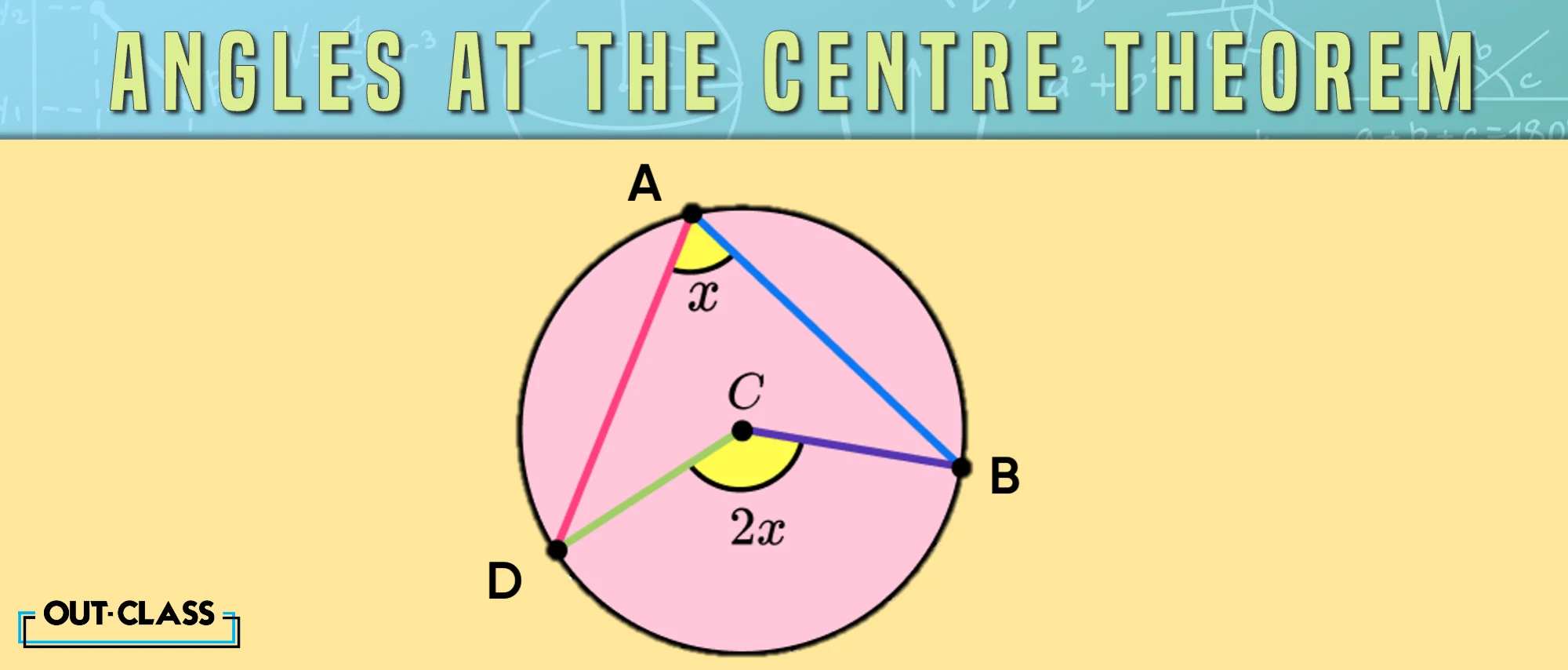
Angle Properties of a Circle - The Angles at the Centre Theorem:
This theorem is like a mathematical "double or nothing" game. It states that the angle formed at the centre of a circle is twice the angle at the circumference.
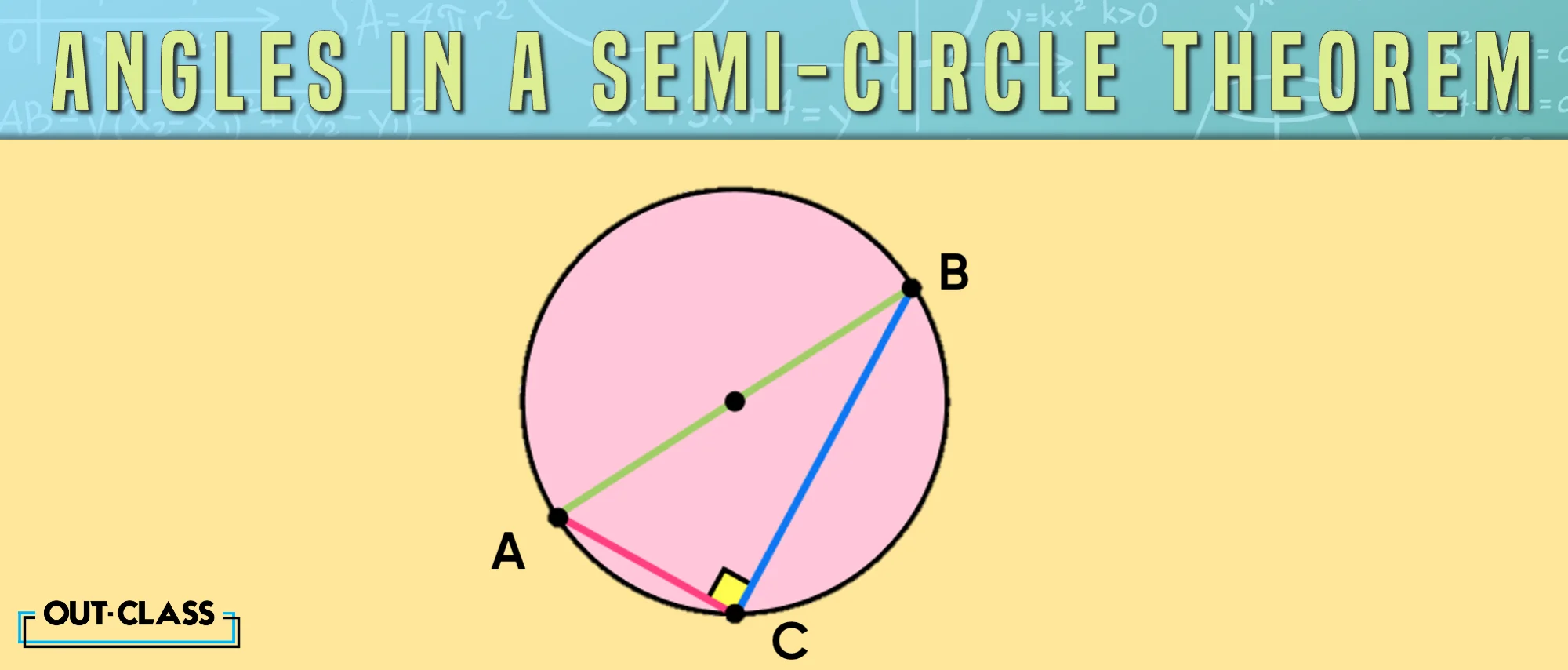
Angle Properties of a Circle - The Angle in a Semicircle Theorem:
In the world of circles, a semicircle is like a secret VIP area with its rules. The Angle in a Semicircle Theorem is simple: the angle formed in a semicircle is always 90 degrees, like a perfectly baked pizza slice!
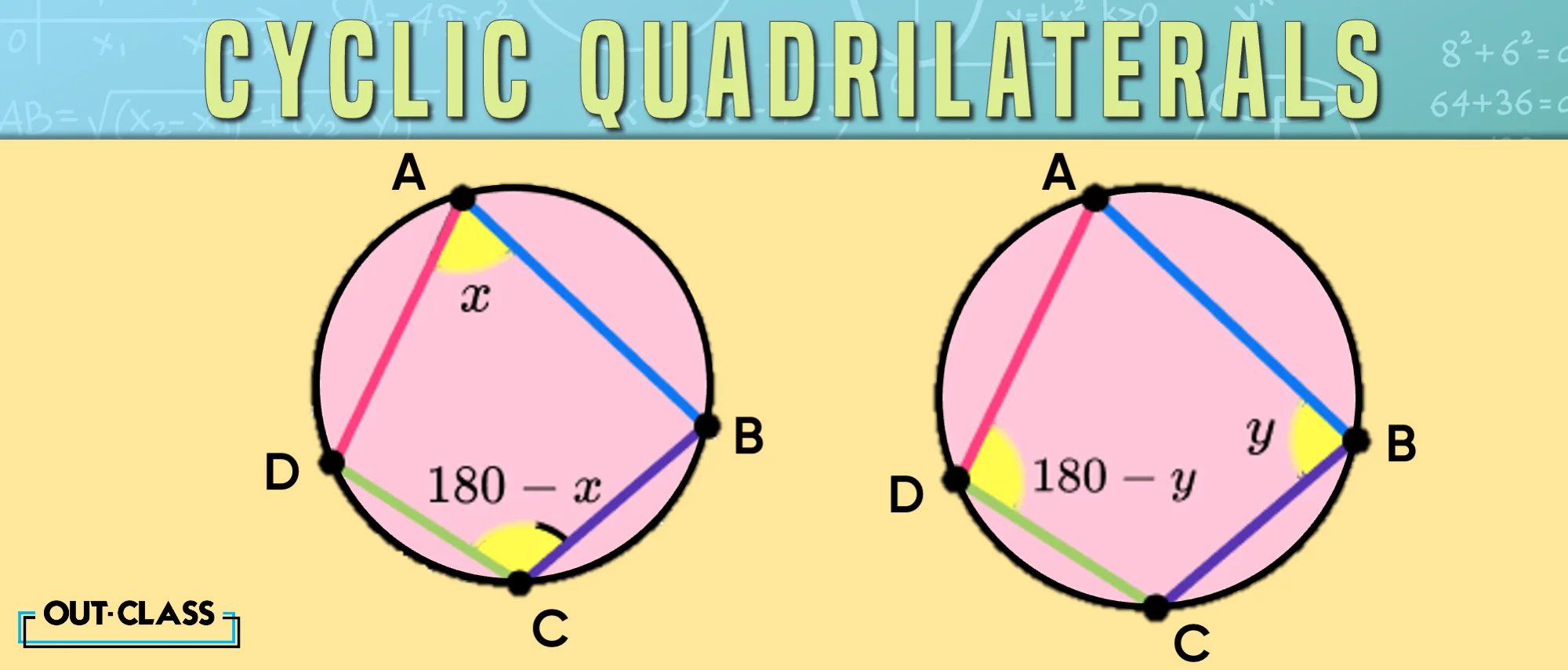
Cyclic Quadrilaterals:
Think of a cyclic quadrilateral as the James Bond of shapes – it always stays on the edge. All its vertices touch the circle's circumference.
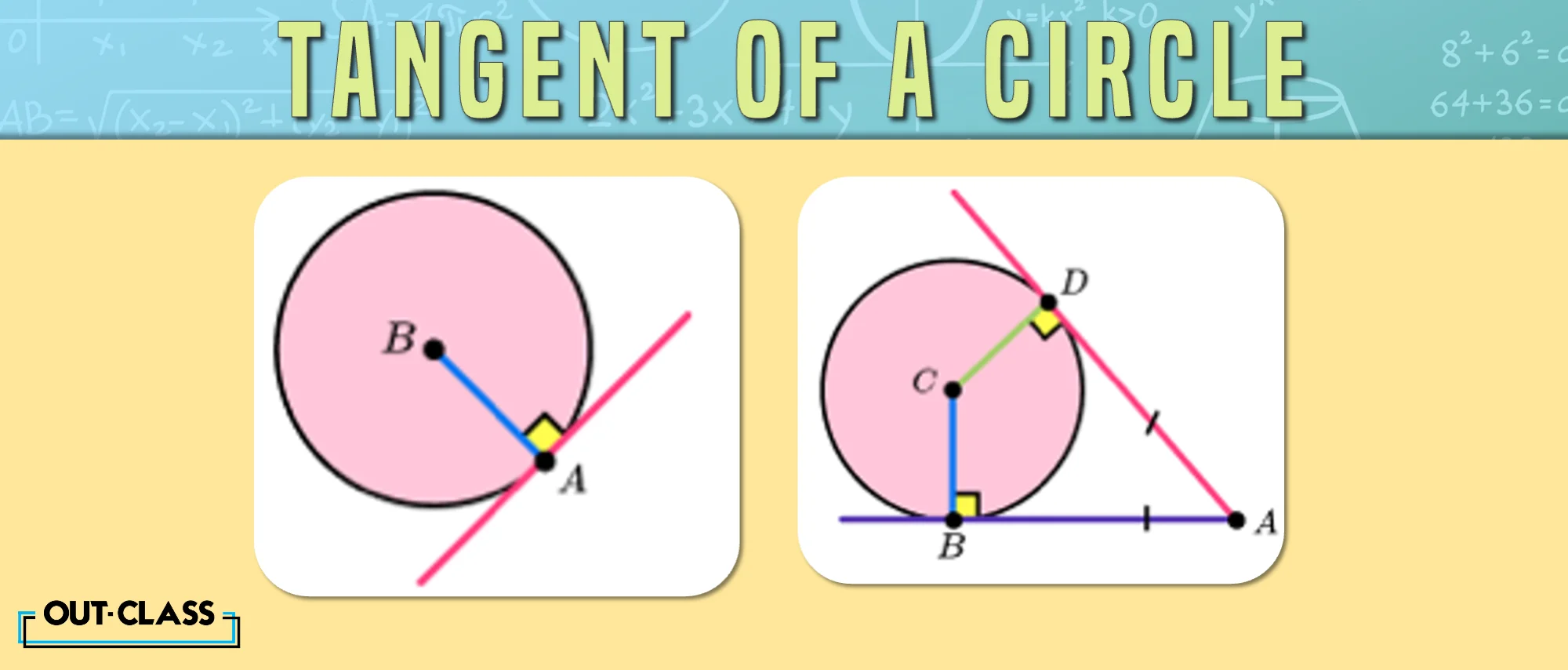
Tangent of a Circle:
Tangents to a circle are like the rebellious teenagers of the geometry world. They touch the circle at just one point and stand perpendicular to the radius, giving circles a run for their money.
Conclusion
Ready to master these circle properties? Dive into your circle properties O Level and IGCSE past papers. Practicing these properties is the key to unlocking your full potential and acing those IGCSE/O Level circle properties questions confidently.
So, there you have it, your ultimate guide to unravelling the properties of a circle. Mathematics may seem like a never-ending circus, but with determination and practice, you'll be the ringmaster of properties of circle O Level.
FAQs:
Q. What are the key angle properties of a circle?
The key angle properties of a circle include:
- The Angle in the Same Segment Theorem: Angles subtending the same arc are equal.
- The Angles at the Centre Theorem: The angle at the center of a circle is twice the angle at the circumference.
- The Angle in a Semicircle Theorem: The angle in a semicircle is always 90 degrees.
- Cyclic Quadrilaterals: All vertices of a cyclic quadrilateral touch the circle's circumference.
Q. What is the definition of a tangent to a circle?
A tangent to a circle is a line that touches the circle at just one point and is perpendicular to the radius at that point.